バッファ・マネジメントについて(8)
「バッファ・マネジメントについて(7)」での考察で出てきた
- 工場サイクルタイムが長くなると「需要の変動に対応するための手持ち在庫数」も増える。
という結論を、確率論的な数式を使って確かめてみます。需要がポアソン過程で発生すると仮定します。ポアソン過程は、事象がまったく無関係に発生する場合で、発生の確率が時間の経過で変化しない場合の発生の仕方です。
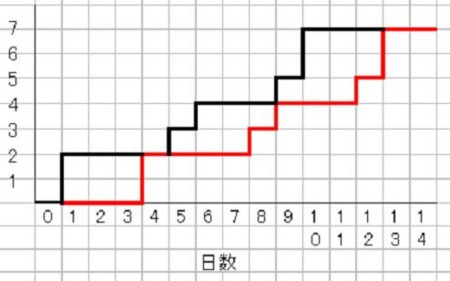
さて、工場サイクルタイムが一定の場合、「バッファ・マネジメントについて(5)」「(6)」で見たように、需要の個数の累計の折れ線を、工場サイクルタイム分、右に(未来に)ズラした折れ線が、製品の製品在庫エリアへの到着回数の累計になるのでした。「バッファ・マネジメントについて(6)」で出したグラフを再度、示します。
黒い折れ線が需要数の累計と、赤い折れ線が到着回数の累計を示しています。そして、黒い折れ線の高さと赤い折れ線の高さの差の最大の値が必要総在庫数になるのでした。と言うことは、ある時点での累積需要数と、その、工場サイクルタイム分過去の時点での累積需要数の差(上のグラフの例では、工場サイクルタイム=3日、です。)の最大値を調べることになります。ということは、その工場サイクルタイムの間に発生する需要の数の最大値を求めることになります。
ポアソン過程の場合、ある期間に平均回発生する事象が、その期間内に
回発生する確率
は、以下の式で与えられます。
・・・・(1)
このの分布がポアソン分布です。さて、この式に厳密に従うならば、どんな大きな
の値でも、それが起こる確率はゼロより大きいです。ということは、たとえば3日の間に、需要がとてつもない数、例えば1万個、発生する可能性も厳密に言えばあります。もっともその確率はとても小さいですが・・・。
ですので、需要の数の最大値を求めようとしても、それは厳密には求められないことになります。そこで、厳密に考えると私たちの日常感覚とズレてしまいますので、最大数の意味を厳密ではなく、たとえば99%以上の確率で、この数より大きくはならない、という意味であるとしてみます。つまり、1%以下の品切れ発生には目をつぶる、ということです。このように考えると、以下のようにして必要在庫数を求めることが出来ます。
最初に工場サイクルタイムが3日の場合を考えます。1日の需要の平均頻度が0.5回でしたので、3日の間に発生する需要の平均回数は3×0.5=1.5回です。よって、式(1)のは
となります。そこで
にいろいろな値を入れて3日の間に需要が
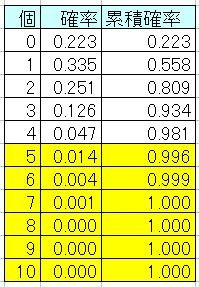
回発生する確率を計算してみます。すると以下の表のような結果になります。
この表から需要の数が5個以下である確率は99%以上(この表からは99.6%)であることが分かります。4個以下である確率は99%には達しませんでした。98.1%でした。従って5個が最大値となります。よって、必要総在庫数は5個です。ところで、「バッファ・マネジメントについて(7)」で述べたように、工場内にある製品の数の平均はリトルの法則から3×0.5=1.5個なので、この場合、製品在庫にある製品の数の平均は5−1.5=3.5個です。
では、今度は工場サイクルタイムが2倍になったとしましょう。つまり6日です。すると、式(1)でのの値が、6×0.5=3回になります。式(1)に
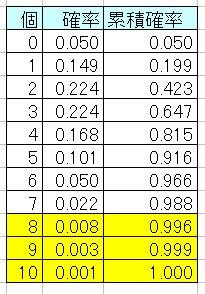
を代入して計算し直すと、下の表にようになります。
この表から、需要の数が8個以下である確率は99%以上だが7個以下である確率は99%未満であることが分かります。よって必要在庫量は8個になります。工場サイクルタイムが2倍になったことで必要総在庫数が5個から8個に増えたわけです。これは、要するに、工場サイクルタイムが長くて需要の変動に追従するのが遅れるために、製品在庫を予め多めに取っておかないと、品切れが発生するからです。先ほどと同様に考えると、工場内にある製品の数の平均はリトルの法則から6×0.5=3個、製品在庫にある製品の数の平均は8−3=5個になります。
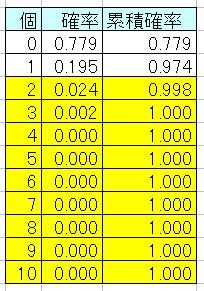
逆に、工場サイクルタイムがもっと短ければ、需要の変動によく追従出来るため、きっと製品在庫にはあまり製品を置かなくても大丈夫になるでしょう。これを確認してみます。工場サイクルタイムが0.5日になったとしましょう。するととなり、式(1)で計算した結果は
になります。この表から必要総在庫数は2個になります。工場内にある製品の数の平均は0.5×0.5=0.25個、よって製品在庫にある製品の数の平均は2−0.25=1.75個、です。