CETが確率的に2値をとる場合のロードポートネック(2)
「CETが確率的に2値をとる場合のロードポートネック(1)」での考察をつづけます。
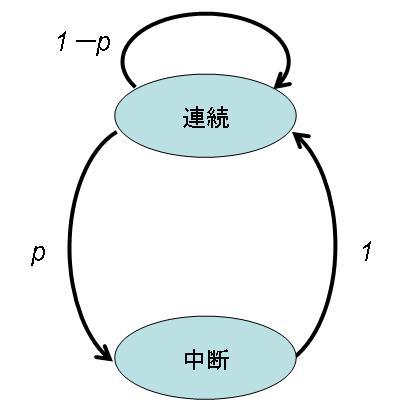
次のロットの処理開始が前のロットの処理終了の直後に行われる状態を「連続」、次のロットの処理開始が前のロットの処理終了からだけ遅れて行われる状態を「中断」と呼ぶことにします。「連続」と「中断」の関係は「CETが確率的に2値をとる場合のロードポートネック(1)」での考察から下図のように書く事が出来ることが分かります。
つまり「中断」状態の次は必ず「連続」状態になり、一方、「連続」状態の時は、次のの値が
になれば「中断」、
になれば「連続」になります。(マルコフ過程ですね。)
このような過程を無限に続けたとして、「連続」と「中断」の出現確率はどのようになるでしょうか? 中断の出現確率を、連続の出現確率を
として、マルコフ過程の定常状態確率を求めるやり方で式を立てると以下のようになります。
・・・・(1)
・・(2)
(1)から
・・・(3)
であることが導かれます。(2)からも同様の式が導かれます。
- (3)から
ならば
、
ならば
になることが分かります。
すると1回の処理には平均して
の空き時間が付随することになります。よって装置のキャパシティは
・・・(3)
となることが分かります。では
(100%)、
では
になります。
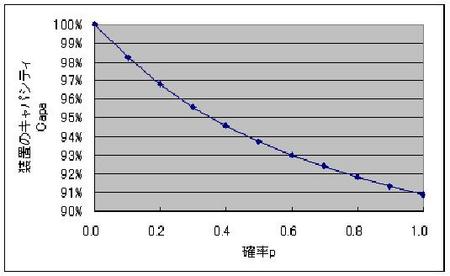
=5分、
=1分とした場合の
と
の関係を下のようにグラフ化しました。
さて、これでが2値を確率的にとる場合の装置キャパシティを求めることが出来ました。しかしこのような考察を
が3つの値をとる場合、4つの値をとる場合・・・、に拡張しようとすると、数が増えるにつれて図5に対応する状態遷移図が複雑になることが分かりました。このため、この考察をもっと一般化することは、今の私には出来ません。
どなたかからサジェスチョンを頂けましたら幸いです。