「プル生産システムのモデル化を目指して（８）」の続きです。
ＴＯＣ（Theory Of Constraint：制約理論）におけるＤＢＲ（ドラム・バッファ・ロープ）はボトルネック・ステーションが、工場の最初の工程へのジョブ投入をプルする一種のプル方針と考えることが出来ます。
今回、「プル生産システムのモデル化を目指して（８）」によってプルすることの効果を明らかにすることは出来ました。次に調べてみたいのは、プルを引き起こす工程がボトルネック・ステーションであることの効果です。
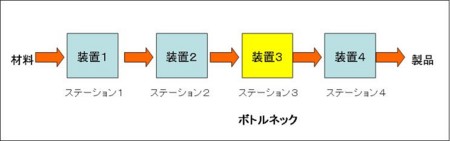
今度は、「プル生産システムのモデル化を目指して（７）」とはちょっと異なる生産ラインを考えます。生産ラインが４つのステーションを直列に並べたものであり、各々のステーションが１台の装置からなることは「（７）」と同じとします。しかし、今度は３番目のステーションがボトルネック・ステーションであるとします。
- 図１
具体的には「（７）」におけるが以下の値をとるとします。
、
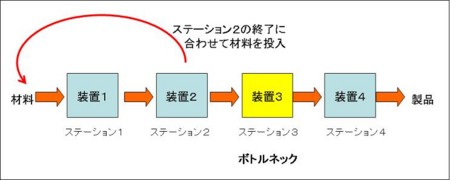
この場合、ＤＢＲであれば、ステーション３でのジョブの処理の終了のタイミングでステーション１へジョブを到着させる、という方針で工場を運用することになります。
- 図２：ケース１（ＤＢＲ適用時）
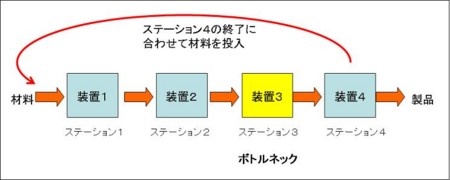
ここで以下の２ケースを考えて、ケース１と比較します。
- 図３：ケース２
- 図４：ケース３
これらよりケース１のほうが、同じボトルネック利用率の条件で比較してX-Factoerが小さければ、「ボトルネック」でプルするというＤＢＲの優位性がはっきりします。
ケース２については、今までどおり
- 図５
のような閉鎖型ジャクソンネットワークに置き換えて「平均値解析法」で解析すれば、解析出来ます。しかし、ケース１や３の場合はこのままでは行きません。ケース１の場合、ステーション１から３までだけの挙動であれば
- 図６
を考えることで解析出来ます。しかしケース４のステーション４の挙動がこれではわかりません。図６におけるステーション３からの出発過程をステーション４に与える必要があります。ステーション３からの出発過程がポアソン過程であると話は簡単なのですが、どうもポアソン過程ではなさそうです。ここで寄り道になりますが、閉鎖型ジャクソンネットワークの、あるステーションからの出発過程について考えてみます。
