ＤＢＲの効果を示すモデル（３） - 工場統計力学（建設中！）

「ＤＢＲの効果を示すモデル（２）」「閉鎖型ネットワーク内のステーションからの出発過程（３）」の続きです。

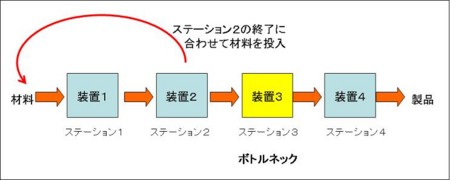
「ＤＢＲの効果を示すモデル（２）」の最後で課題となっていた下図の

図１０

閉鎖型ジャクソンネットワークのステーション２からの出発過程の２乗変動係数を、「閉鎖型ネットワーク内のステーションからの出発過程（３）」の式（２７）（ここでは式（１）と番号を振り直します。）

$c_d^2=1-\frac{2}{(n+1)^2}$ ・・・・・（１）

で求めることが出来ました。この結果を用いて、ケース３

図４：ケース３

の $u$ （利用率）− $x$ （X-Factoer）関係の解析を続けます。

「プル生産システムのモデル化を目指して（６）」の式（３０）（ここでは式（２）と番号を振り直します。）

$u(w)=\frac{w}{w+N-1}$ ・・・・・（２）

を図１０のネットワークに適用すると $N=2$ なので

$u_1=u_2=\frac{n}{n+1}$ ・・・・・（３）

つまり、装置１と装置２での総ジョブ数 $n$ で装置１と２の利用率 $u_1=u_2$ が定まります。ところで

$t_{e1}=t_{e2}=t_{e4}=0.8$ 、 $t_{e3}=1$

と仮定していましたので、 $u_1=u_2{\le}0.8$ です。それ以上になると装置３の利用率 $u_3$ が１を越えてしまいます。このことと式（２９）から許される $n$ の値は１，２，３，４だけであることが分かります。それぞれの値の時の $u_3$ の値を計算してみると

$n=1$ で $u_3=0.63$
$n=2$ で $u_3=0.83$
$n=3$ で $u_3=0.94$
$n=4$ で $u_3=1.00$

となります。 $u_3=1.00$ ではステーション３のサイクルタイム $CT_3$ が無限大になってしまいますので、ケース３の $u$ − $x$ 関係を求めるために計算する必要のある場合は、
$n=1,2,3$ の場合のみであることが分かります。これらの時の装置２からの出発過程の２乗変動係数 $c_{d2}^2$ を式（１）を用いて計算すると次のようになります。

$n=1$ で $u_3=0.63$ 、 $c_{d2}^2=0.50$
$n=2$ で $u_3=0.83$ 、 $c_{d2}^2=0.78$
$n=3$ で $u_3=0.94$ 、 $c_{d2}^2=0.88$

また、 $c_{d2}=c_{a3}$ なのでこれらのデータを用いて、Kingmanの近似式

$CT_{q3}=\frac{c_{a3}^2+1}{2}\frac{u_3}{1-u_3}t_{e3}$

を適用すれば、ステーション３での待ち時間 $CT_{q3}$ を求めることが出来ます。これに処理時間 $t_{e3}$ を足せば、ステーション３でのサイクルタイム $CT_3$ を計算することが出来ます。次につなぎの式

$c_{a4}^2=c_{d3}^2=u_3^2c_{e3}^2+(1-u_3^2)c_{a3}^2=u_3^2+(1-u_3^2)c_{a3}^2$

を用いて $c_{a4}^2$ を計算し、ふたたびKingmanの近似式

$CT_{q4}=\frac{c_{a4}^2+1}{2}\frac{u_4}{1-u_4}t_{e4}$

を適用して、ステーション４での待ち時間 $CT_{q4}$ を求め、ステーション４でのサイクルタイム $CT_4$ を計算することが出来ます。また、「プル生産システムのモデル化を目指して（６）」の式（２７）から

$CT_1+CT_2=(n+1)t_{e1}$

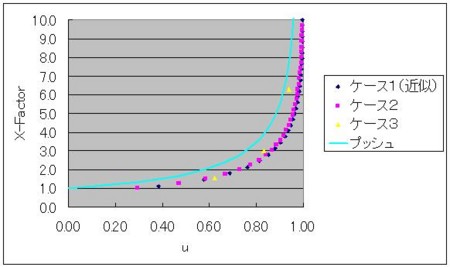
これらから、このラインのサイクルタイム $CT$ を計算することが出来ます。ここからX-Factoer $x$ を計算します。これで $u$ − $x$ 関係を求めることが出来ます。（ここでの $u$ は今までと同じくボトルネックでの利用率。この場合は $u_3$ ）。その結果を下のグラフに示します。このグラフにはケース１，２の場合も一緒に描いてあります。また、プッシュの場合も一緒に描いてあります。

図１１

その一部を拡大したグラフは

図１２

となります。これらのグラフから分かるように、やはり、ボトルネックからプルするケース１が一番X-Factoerが小さくなることが判明しました。
これでＴＯＣのＤＢＲ（ドラム・バッファ・ロープ）方針の有効性を数学的モデルで確かめることが出来ました。

今までのまとめを「ＤＢＲの効果を示すモデル（４）」に示します。