リトルの法則の証明
リトルの法則、すなわち
の証明は、サイクルタイムとスループットが一定値の場合(すなわち変動がない場合)であれば、直感的に分かります。
サイクルタイムとスループットが一定の場合
サイクルタイムとスループットが一定ではない場合も含むように拡張する。
-
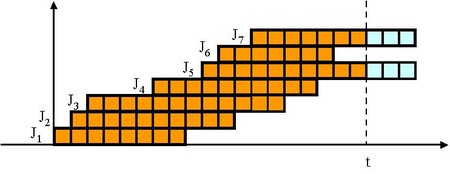
- この図でジョブ
よりあとに到着したジョブ
が
より先に終わっているのに注意して下さい。サイクルタイム(
)に変動があるために、このようなケースもあり得ることをこの図で考慮しています。
- この図でジョブ
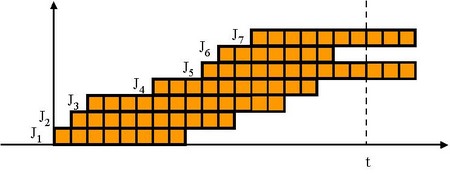
- 次に時刻0から時刻
までに到着したジョブのサイクルタイムの合計を考えます。この例の場合、時刻0から時刻
までに到着したジョブは
〜
です。よって、それらのジョブのサイクルタイムの合計は、下図のオレンジ色の部分の面積になります。
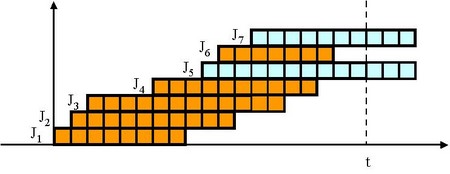
- さらに時刻0から時刻
までに完了してラインから出ていったジョブのサイクルタイムの合計を考えます。この例の場合、時刻0から時刻
までに到着したジョブは
〜
と
です。よって、それらのジョブのサイクルタイムの合計は、下図のオレンジ色の部分の面積になります。
- この3つの図を比べると、
- が成り立つことが分かります。この式を
で割ると
- となります。ここで
とすると
- となり、その結果
- となるので
- となります。これでリトルの法則の証明が出来ました。
で、完了数/
も、到着数/
も、平均スループットに収束するところがミソですね。